拉格朗日力学--经典双摆的案例

一、系统建模与参数定义

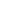
考虑由两根无质量刚性杆组成的平面双摆：

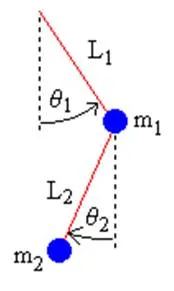
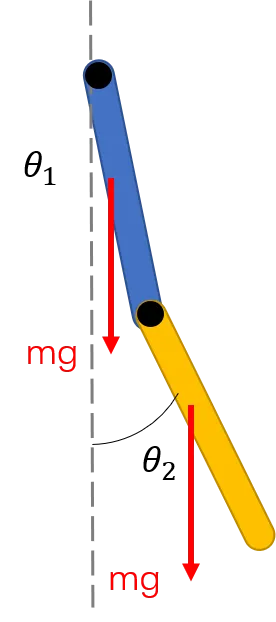
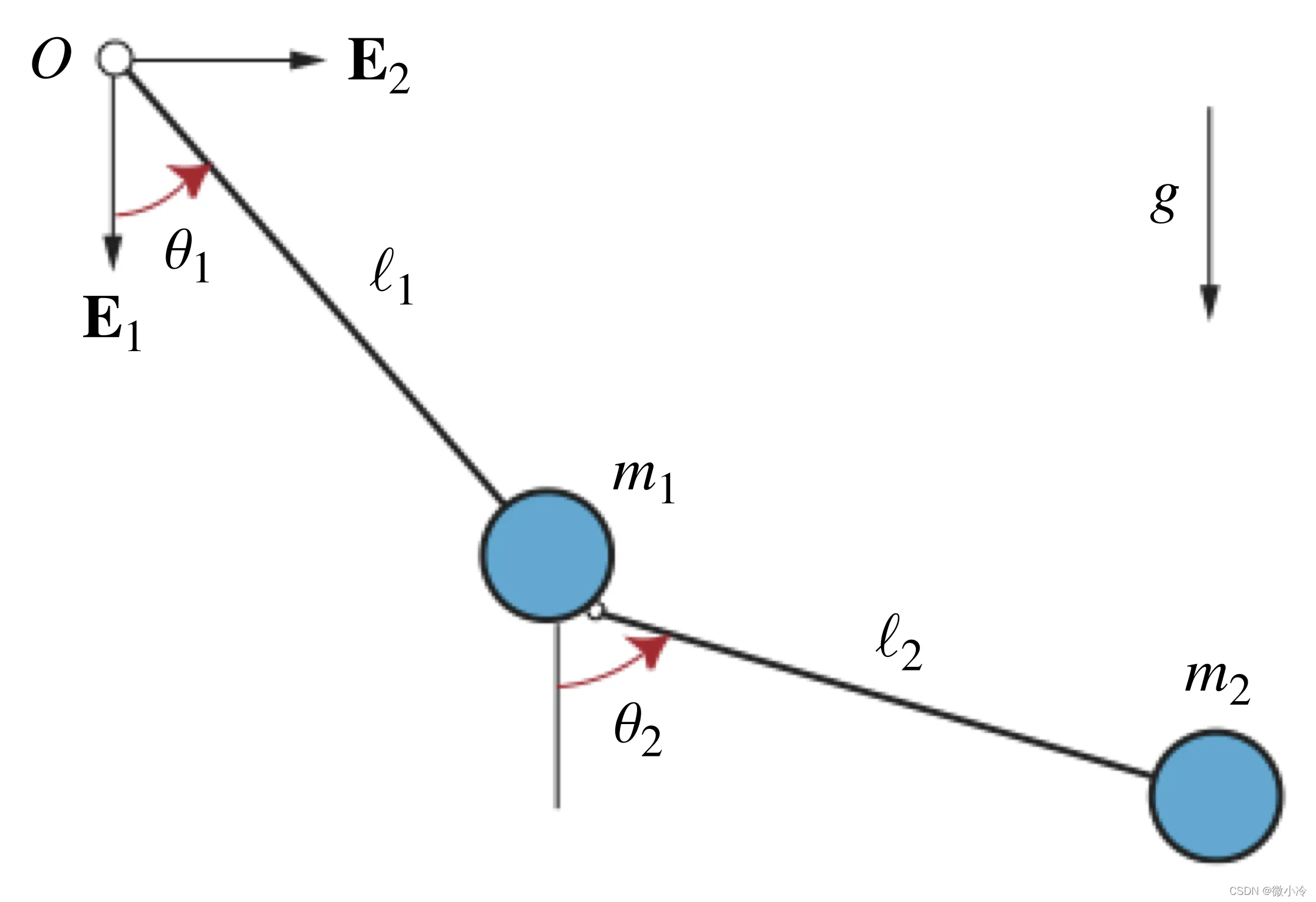
上端杆长\\(L_1\\)，下端连接质量\\(m_1\\)的小球

下端杆长\\(L_2\\)，末端连接质量\\(m_2\\)的小球

两杆与竖直方向夹角分别为\\(\theta_1\\)、\\(\theta_2\\)（广义坐标，2 个自由度）

重力加速度为\\(g)，系统无摩擦约束

二、拉格朗日量构建（L=T-V）

1. 动能计算（平动动能总和）

通过坐标变换将小球位置表示为广义坐标的函数：

x₁ = L₁sinθ₁,  y₁ = -L₁cosθ₁
x₂ = L₁sinθ₁+L₂sinθ₂,  y₂ = -L₁cosθ₁-L₂cosθ₂

对时间求导得速度分量，动能为：

(T = \frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2) + \frac{1}{2}m_2(\dot{x}_2^2+\dot{y}_2^2))

化简后：

(T = \frac{1}{2}(m_1+m_2)L_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2L_2^2\dot{\theta}_2^2 + m_2L_1L_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2))

2. 势能计算（重力势能总和）

以悬挂点为势能零点：

(V = m_1gL_1(1-\cos\theta_1) + m_2g[L_1(1-\cos\theta_1)+L_2(1-\cos\theta_2)])

3. 拉格朗日量确立

(L = T - V = \left[ \frac{1}{2}(m_1+m\_2)L_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2L_2^2\dot{\theta}_2^2 + m_2L_1L_2\dot{\theta}\_1\dot{\theta}_2\cos(\theta_1-\theta_2) \right]

- \left[ (m_1+m_2)gL_1(1-\cos\theta_1) + m_2gL_2(1-\cos\theta_2) \right])

三、欧拉 - 拉格朗日方程求解

对两个广义坐标分别应用方程：

(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}_i}\right) - \frac{\partial L}{\partial \theta_i} = 0\\)

1. 关于θ1的方程

• 计算偏导数：

(\frac{\partial L}{\partial \dot{\theta}\_1} = (m_1+m_2)L_1^2\dot{\theta}_1 + m_2L_1L_2\dot{\theta}_2\cos(\theta_1-\theta_2)\\)

\\(\frac{\partial L}{\partial \theta_1} = -m_2L_1L_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2) - (m_1+m_2)gL_1\sin\theta_1\\)

• 时间导数与整理后得：

\\((m_1+m_2)L_1\ddot{\theta}_1 + m_2L_2\cos(\theta_1-\theta_2)\ddot{\theta}_2 + m_2L_2\sin(\theta_1-\\theta\_2)\dot{\theta}_2^2 + (m_1+m_2)g\sin\theta_1 = 0 \quad (1))

2. 关于θ2的方程

同理推导得：

(L_2\ddot{\theta}_2 + L_1\cos(\theta_1-\theta_2)\ddot{\theta}_1 - L_1\sin(\theta_1-\theta_2)\dot{\theta}_1^2 + g\sin\theta_2 = 0 \quad (2)\\)

四、物理意义与拓展

1. 非线性特性：
2. 方程 (1)(2) 含\\(\sin(\theta_1-\theta_2)\\)等非线性项，大摆角时表现混沌行为（对初始条件极度敏感）
3. 简化特例：
4. 当\\(m_2=0\\)时退化为单摆方程\\(L_1\ddot{\theta}_1 + g\sin\theta_1=0\\)
5. 工程关联：弹性双摆模型（杆具弹性形变）可用于柔性机械臂、仿生运动研究
6. 数值验证：通过 Python 的odeint函数求解微分方程，可绘制动图展示轨迹演化